A EQUAÇÃO DE CÁLCULO DA DISTÂNCIA
O RADAR utiliza o princípio da propagação de uma onda eletromagnética e a sua reflexão em um alvo de interesse, para descobrir três parâmetros do alvo: sua distância da antena do RADAR, seu azimute em relação aos 360° ao redor da antena e a altura do alvo.
Para calcular a distância (R) entre a antena do RADAR e o alvo é necessário emitir e captar uma onda eletromagnética com potência suficiente para excitar o sensor no receptor, como podemos observar na figura abaixo:
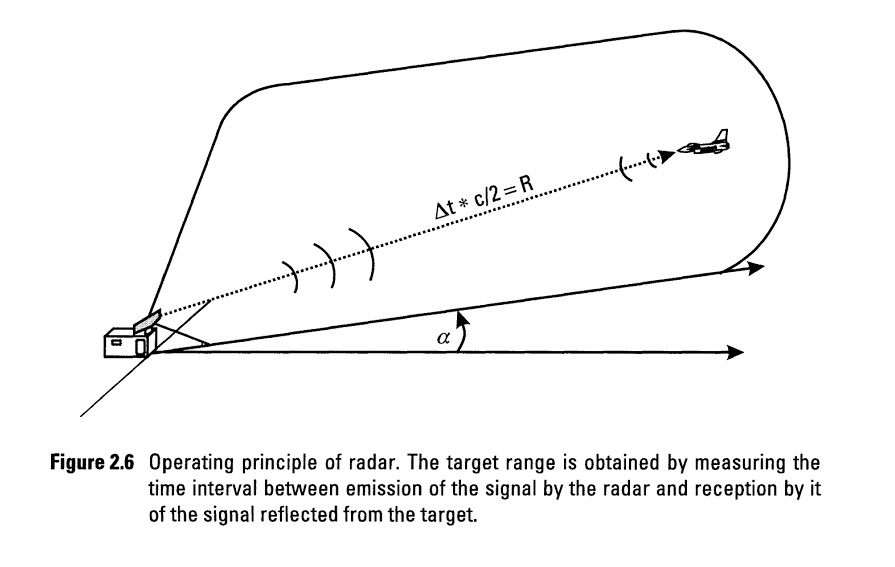
A distância entre a antena do RADAR e o alvo pode ser estimado considerando o intervalo de tempo (Δt) entre a emissão e a detecção. Se medirmos esse intervalo de tempo, considerando que a velocidade de propagação de uma onda eletromagnética é a velocidade da luz (c ≈ 300.000.000m/s), ao dividir por dois, teremos a distância (R) antena alvo [pois a onda eletromagnética vai e volta (2R)].
As medidas de azimute e altura (ângulo de inclinação) não dependem de cálculo, mas de características dos feixes de detecção da antena do RADAR, como podemos observar nas figuras abaixo:
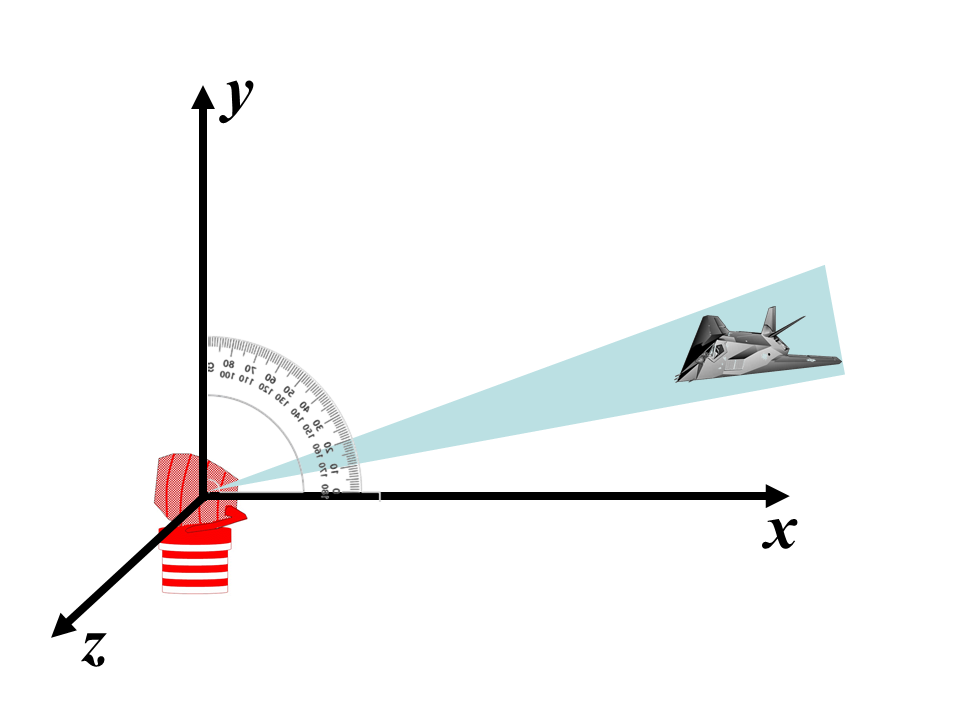
A detecção de um alvo depende, fundamentalmente, das características da antena do Sistema RADAR. Se o feixe da antena do RADAR for muito diretivo, ou seja, emita em uma direção bem estreita, poderemos determinar onde está a aeronave alvo, em relação a esse ponto.
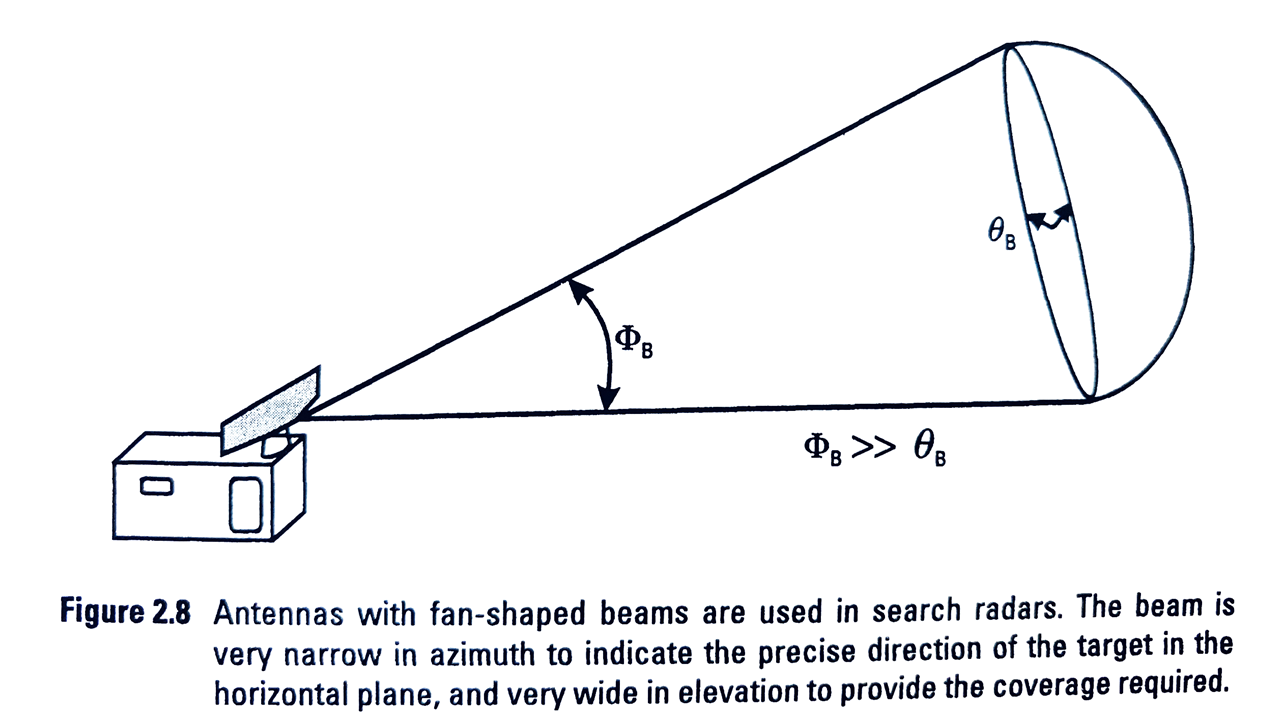
Normalmente, RADARES de Controle de Tráfego Aéreo usam antenas de alta precisão em relação ao azimute, porém, com uma abertura enorme em relação à elevação. Dessa forma, ele garante a detecção do alvo em diversas alturas, com a segurança de conseguir determinar sua posição nos 360° ao redor da antena, com precisão, conforme a figura abaixo:
PROPAGAÇÃO NO ESPAÇO LIVRE
O modelo de propagação no espaço livre considera dois sistemas, um emissor e um receptor, em linha de visada direta, sem obstrução, em um meio isotrópico. Esse modelo é usado para prever a intensidade do sinal (potência) que se propaga, normalmente encontrados nos sistemas de Comunicações por Satélite, Enlace de Dados em Micro-ondas, comunicações e navegação aeronáuticas, entre outros.
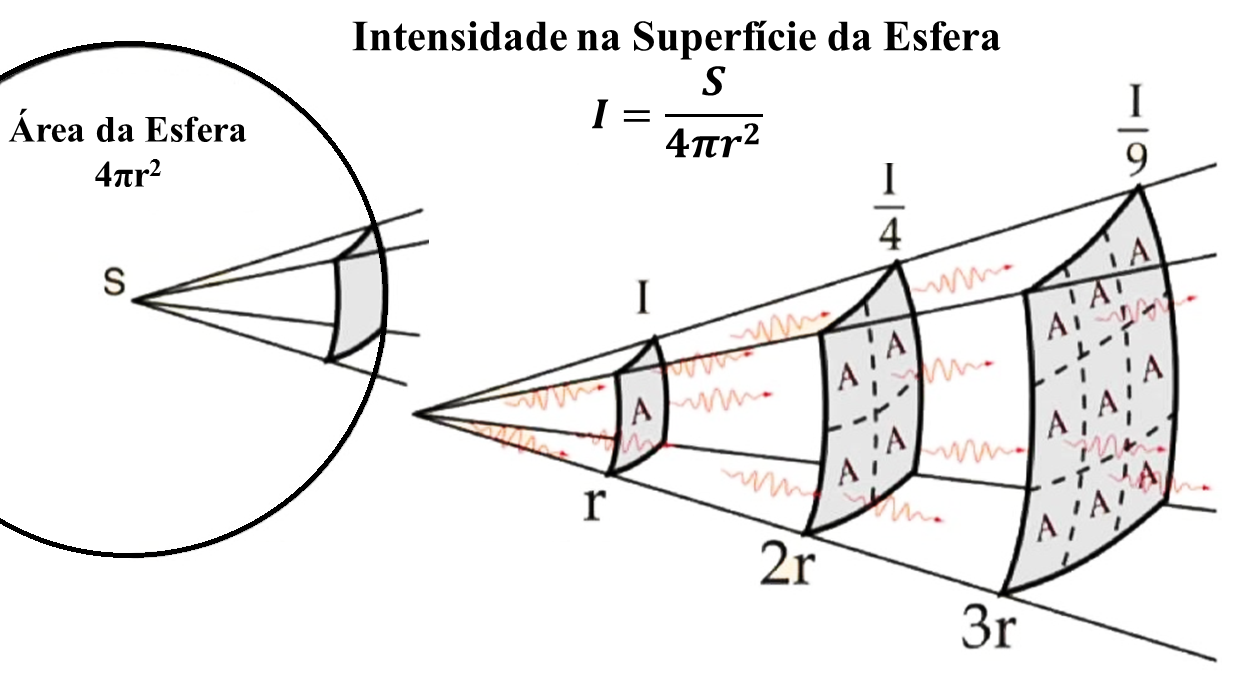
A potência recebida (Pr) pode ser descrita pela seguinte equação, em função da distância (d):
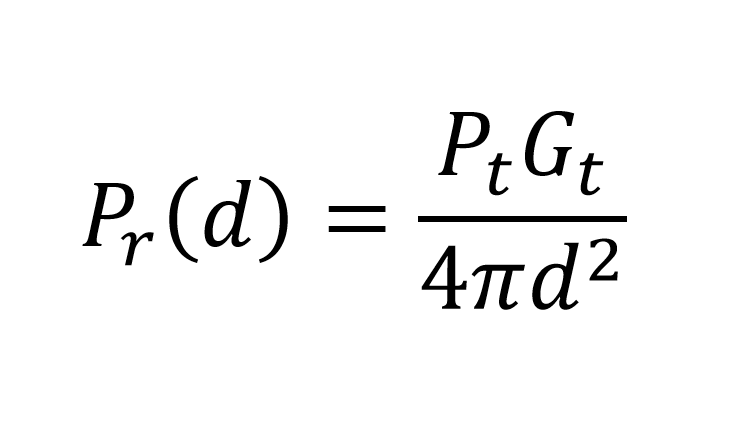
Onde Pr (d) é a potência recebida em função da distância (d), Pt é a potência transmitida, Gt é o ganho da antena transmissora e d é a distância. O fator ” 4πd2 ” no denominador corresponde ao Lei do Inverso do Quadrado da Distância, que estabelece que a energia propagada em uma direção diminui com o aumento da distância. Na figura abaixo, podemos observar facilmente porque isso ocorre:
REFLEXÃO EM UM ALVO
Quando uma onda eletromagnética incide em um alvo, parte da energia que chega no alvo é refletida em direção a antena receptora, de forma a permitir que o alvo seja localizado.
A razão entre a potência refletida pelo alvo e a potência que incide no alvo é chamada de Seção Reta Radar (RCS, do inglês RADAR Cross Section). Ela é representada por σ (letra grega sigma). Por ser uma razão, não possui grandeza associada. Inserindo na equação de propagação no espaço livre, temos:
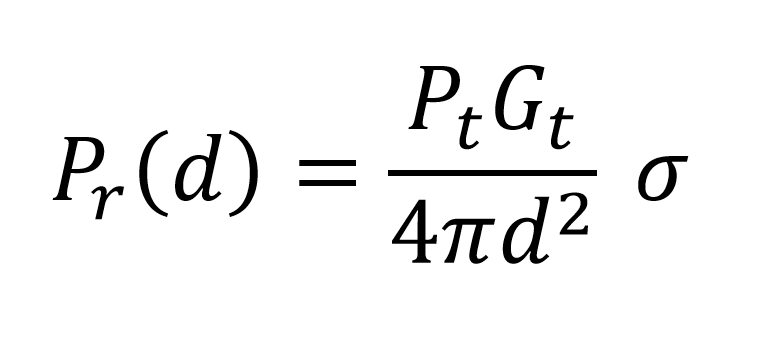
Considerando que a onda eletromagnética se propaga, novamente, do alvo até a antena receptora, temos a seguinte equação para a potência recebida:
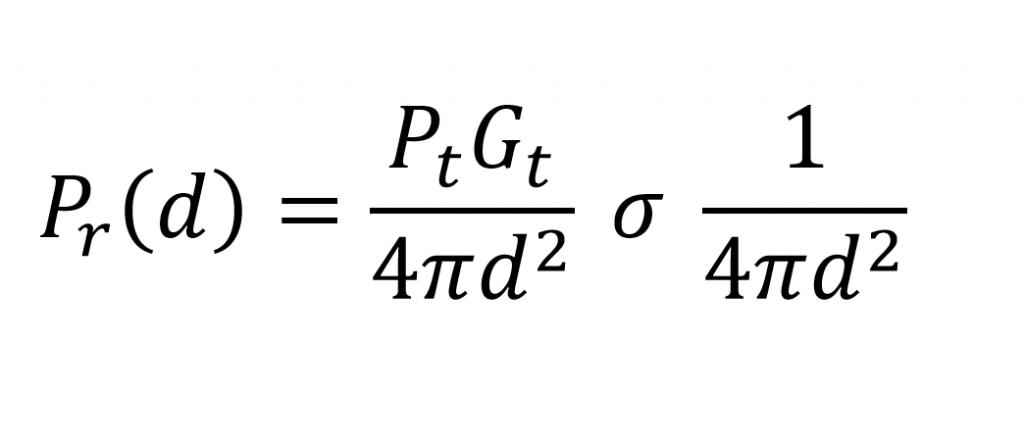
Nesse ponto, analisamos a onda eletromagnética que incide na antena receptora, onde temos a seguinte representação matemática:
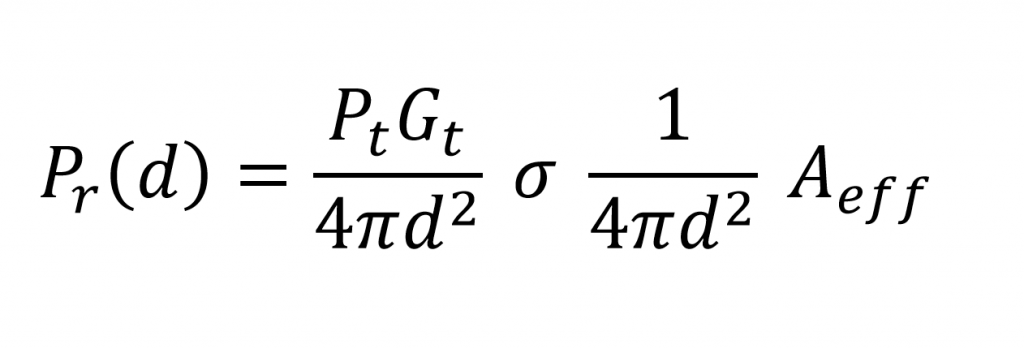
Onde Aeff é a área efetiva da antena receptora, considerando que o Sistema RADAR é Biestático, ou seja, possuí duas antenas diferentes. Dessa forma, substituindo a Aeff por sua expressão matemática, temos a seguinte fórmula:
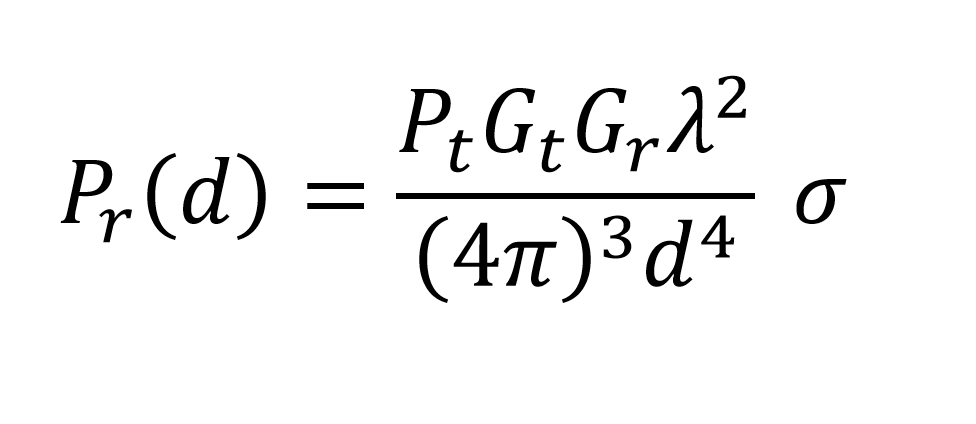
Onde Gr é o ganho da antena receptora e λ é o comprimento da onda em metros. Note que o comprimento de onda é uma variável importante para aumentar a potência recebida, porém, nessa equação não consideramos as perdas pela absorção atmosférica.
HORIZONTE RÁDIO
Na superfície terrestre, o problema do alcance RADAR é limitado pelo horizonte rádio, ou seja, a distância máxima em que a curvatura da Terra permite que dois sistemas consigam estabelecer uma linha de visada sem obstáculos. Essa distância pode ser calculada pela seguinte equação:

Para distância maiores que d, não haverá comunicação entre os sistemas.
Referências:
F. Neri, Introduction to Electronic Defense Systems (2nd Edition), SciTech Publishing: Raleigh, 2006, pg 44-50.