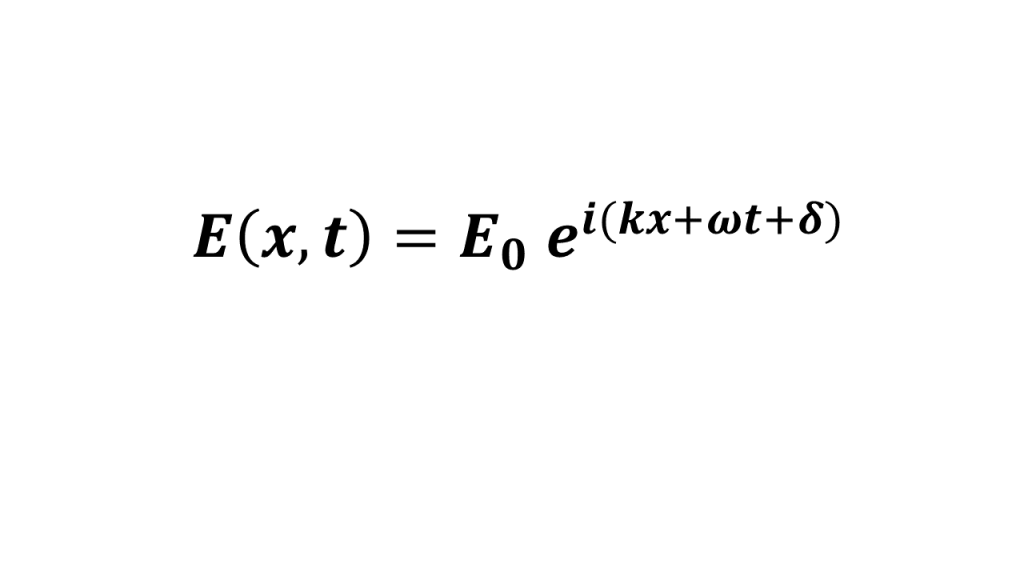Quando uma pedra é atirada em um lago muito calmo, ao incidir na superfície plana da água, a pedra altera a posição das partículas de água, provocando uma perturbação, que se propagará por todo o lago.
Esta perturbação se propagará em todas as direções, de maneira uniforme, na forma de ondas concêntricas se afastando do ponto de impacto, com a mesma velocidade e intensidade, conforme ilustrado na imagem abaixo:

Da mesma forma, quando um martelo de um sino incide sobre a sua superfície, temos o surgimento de uma perturbação mecânica no ar, que se propaga imediatamente concêntrica ao local do impacto, em três dimensões.
As características de propagação de uma onda depende fundamentalmente das propriedades do meio em que ela se propaga.
DESCRIÇÃO MATEMÁTICA DAS ONDAS SENOIDAIS
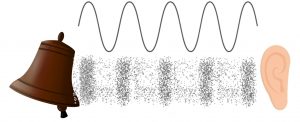
Essa é a representação gráfica, em duas dimensões, de uma onda senoidal se propagando no Plano Cartesiano:
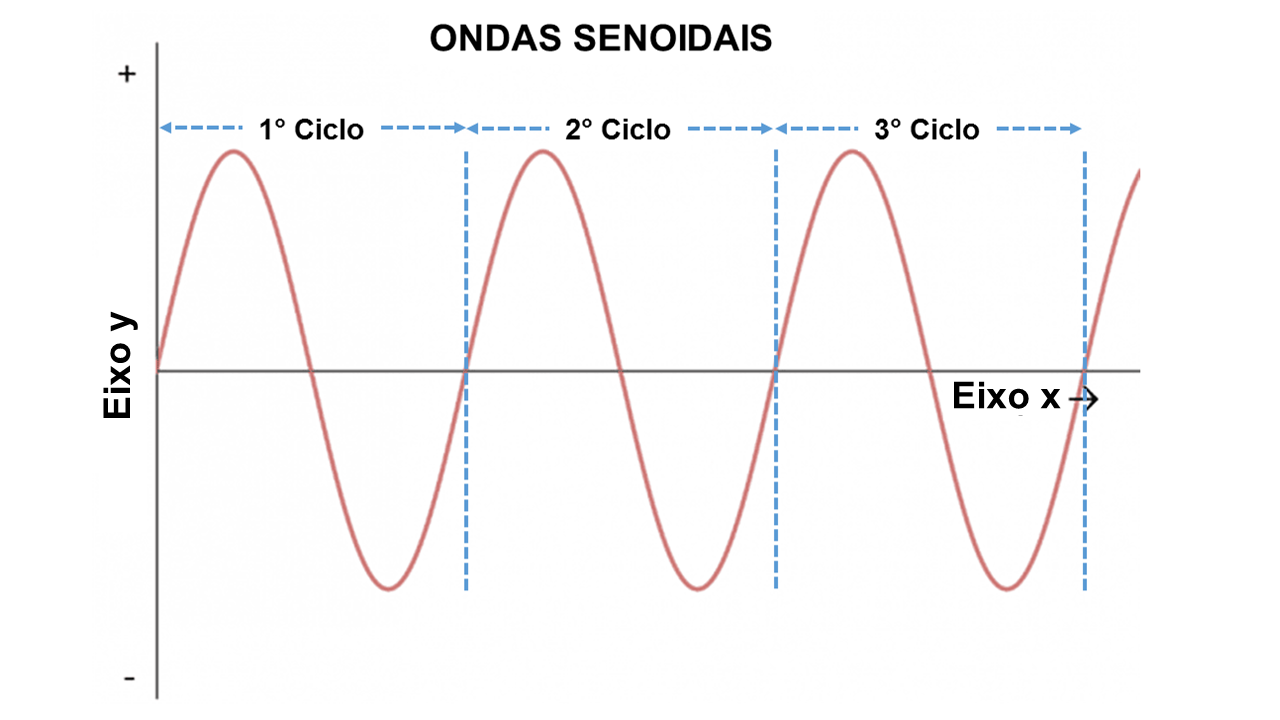
O eixo das abcissas representa a quantidade de perturbação e o eixo das ordenadas corresponde a uma posição espacial ou temporal. Podemos observar que a forma da curva no primeiro ciclo se repete nos demais ciclos, ou seja, a perturbação se desloca no eixo x, sem sofrer deformação.
Se considerarmos o eixo x uma dimensão espacial, então podemos representar a velocidade de deslocamento da onda, para o sentido positivo, como sendo:
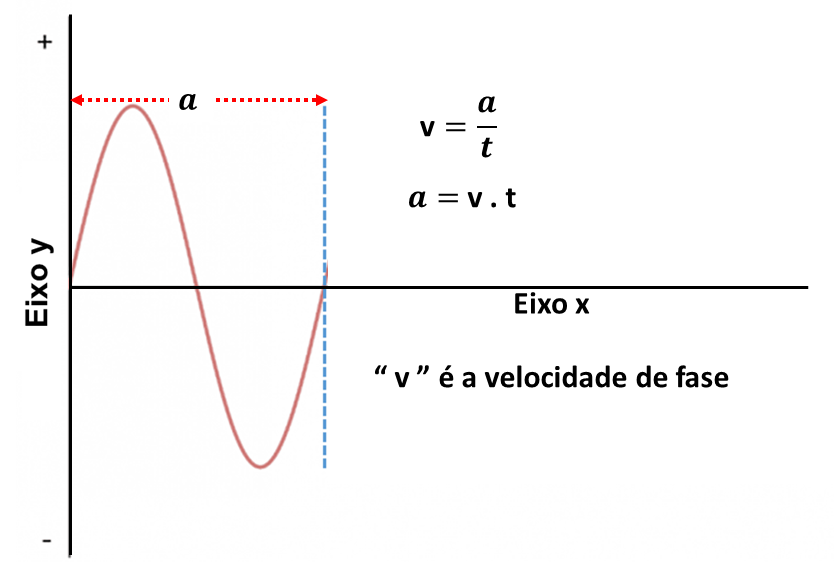
Onde ” v ” é a velocidade de fase, pois corresponde ao deslocamento da frente de onda em relação ao tempo ” t “.
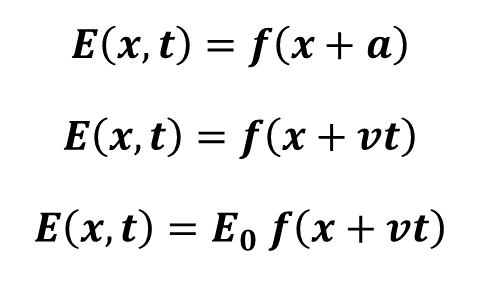
Uma equação que descreve exatamente a oscilação acima é a função trigonométrica seno. Dessa forma temos a seguinte equação:
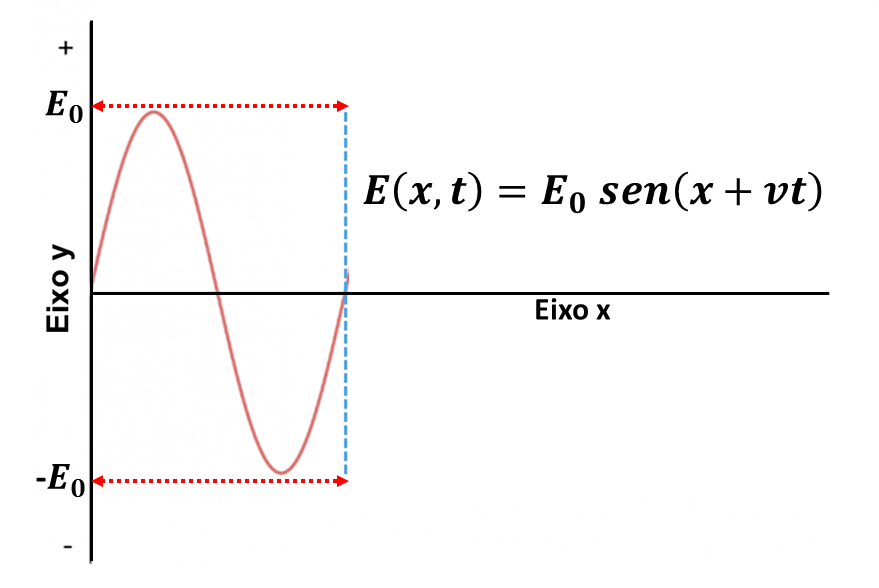
Outros dois conceitos interessantes para definirmos o deslocamento de uma onda. O primeiro é o comprimento de onda, que é a distância no eixo x, na direção de propagação da onda medida entre repetições da forma da onda, ou seja, corresponde à distância entre duas cristas ou dois vales. O seu inverso é o chamado número de onda, que é o números de comprimentos de onda por unidade de distância.
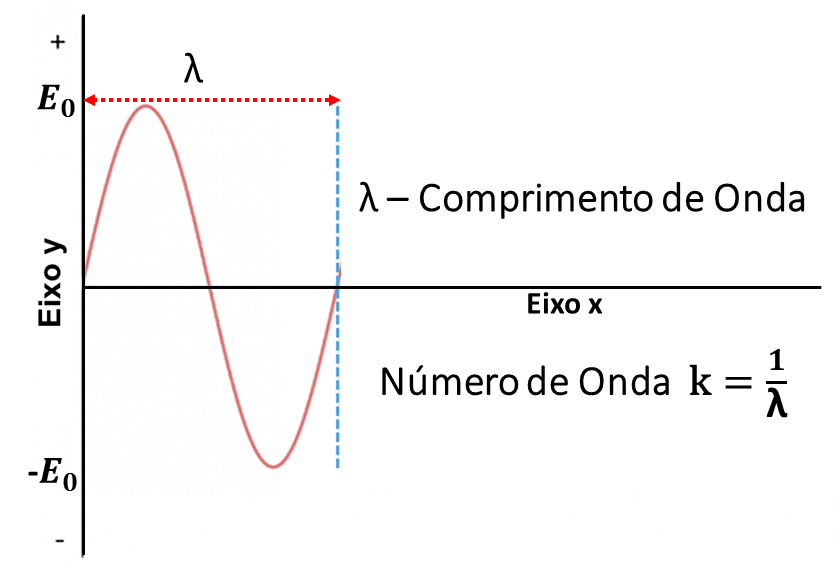
A frequência é a grandeza que define quantos ciclos ocorrem em um determinado intervalo de tempo, ou período. Se a onda corresponde a uma oscilação harmônica simples, temos a frequência angular, que varia de 0 à 2π.
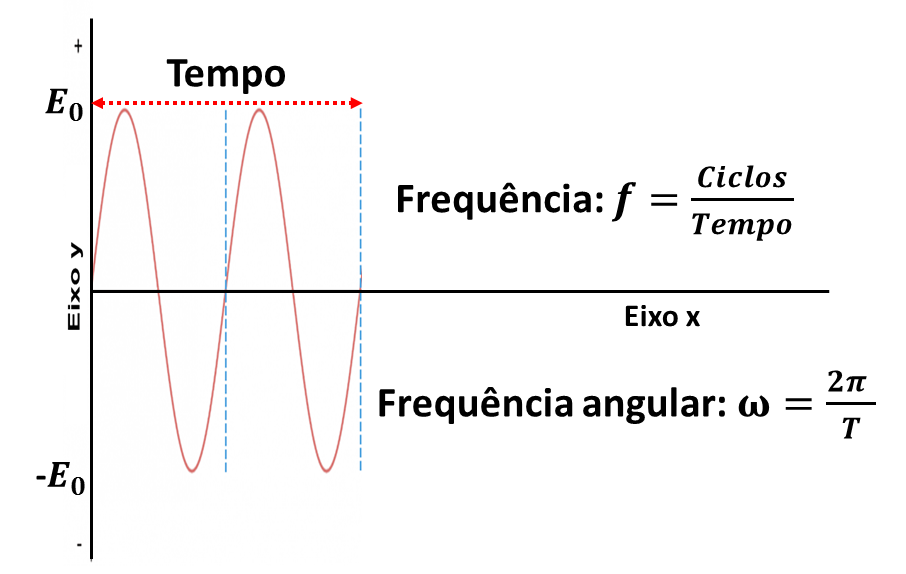
Dessa forma, temos a equação final da onda em um movimento harmônica simples:

Se incluirmos os conceito de números complexos, considerando a parte imaginária, podemos representar as ondas pela função exponencial com argumento puramente imaginário, na seguinte expressão, que representa o deslocamento no eixo x de uma onda eletromagnética plana: